Kotlin实现的二叉树数据结构

二叉树，树，二叉，倒树

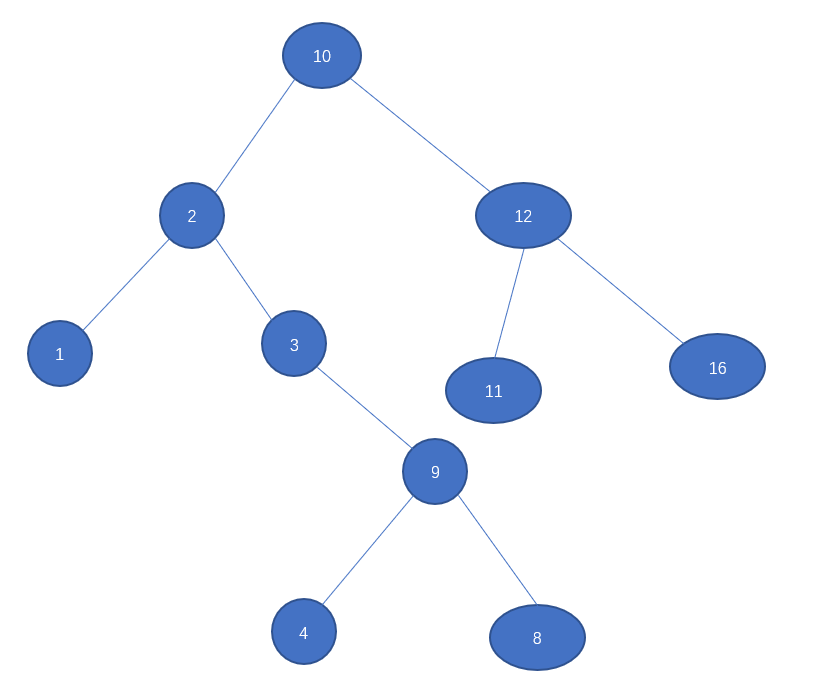
小的key在左边，大的数在右边。

每个节点下可以有一个/两个节点

那就看看我们怎么实现这个数据结构吧

设计

一般来说，我们在写一个数据结构之前，先有思想，然后设计API。

BinaryTree 类

节点Node类

API设计

也就是BinaryTree的API设计，暴露什么方法出去。

• put(key:K,value:V) 添加数据
• delete(key:K):Node<K,V>? 删除节点
• get(key:K):Node<K,V>? 查找某个节点，有可能为null
• minKey():Node<K,V>? 查找key最小的节点
• maxKey():Node<K,V>? 查找key最大值的节点
• getDepthSize() 获取最大深度
• size() 节点数量
• 各种遍历方式

添加数据

/**
     * 添加节点
     */
    fun put(key: K, value: V) {
        root = put(root, key, value)
    }

    /**
     * 在某个节点下添加内容
     */
    private fun put(node: Node<K, V>?, key: K, value: V): Node<K, V> {
        if (node == null) {
            size++
            return Node<K, V>(key, value, null, null)
        }
        //判断在左边还是右边还是当前的位置
        //如果是当前的位置，那么就改值
        val cmp = key.compareTo(node.key)
        when {
            cmp < 0 -> {
                //在左边，递归调用，如果left为null的话，直接就返回了node了
                node.left = put(node.left, key, value)
            }
            cmp > 0 -> {
                //在右边
                node.right = put(node.right, key, value)
            }
            else -> {
                node.value = value
            }
        }
        return node
    }

要点是： - 有不有root - 放在左边还是右边 - 递归思想 - size要记得更新

添加的逻辑已经写在注释里了，脑补一下图哈。

查找节点

查找节点的时候，我们有key，还有root

这个好办，我们对比一下在左边还是右边即可，如果key一样，就是了。如果没有一样的，那就返回null了。

代码实现：

    /**
     * 获取内容
     */
    fun get(key: K): Node<K, V>? {
        return get(root, key)
    }

    /**
     * 在某个节点下获取节点
     */
    private fun get(node: Node<K, V>?, key: K): Node<K, V>? {
        if (node == null) {
            return null
        }
        //判断左右还是自己
        val cmp = key.compareTo(node.key)
        return when {
            cmp < 0 -> {
                //取左边
                get(node.left, key)
            }
            cmp > 0 -> {
                //取右边
                get(node.right, key)
            }
            else -> {
                //自己
                node
            }
        }
    }

删除数据

删除数据的话会比较复杂一点，也是递归思想。难点的话应该是在删除中间某个节点，然后得拼接回去。

思考之前可以先想一下case，传入的参数有key，你手上有的是root。怎么样去查找呢？找到以后还要删除，删除以后还要拼接。

设当前元素=要删除的元素

• 除了删除root，都是有父节点的，删除的方式就是通过父节点置空目标节点
• 如果当前元素没有左节点，没有右节点，直接删除，也就是直接通过父节点置空（left/right = null）
• 如果当前元素有左节点，没有右节点，那么就将当前节点的左节点链接到父节点（left/right=target.left）
• 如果当前节点有右节点，没有左节点的，那么就将当前的节点右节点链接到父节点（left/right=target.right）
• 如果当前元素有左节点和右节点，那么就拿到右节点的最小值替换当前节点，替换包括着链接当前节点的左右节点以及拼接到父节点。
• size要进行更新

通过递归的实现方式如下：

 /**
     * 删除节点
     */
    fun delete(key: K): Node<K, V>? {
        return delete(root, key)
    }

    private fun delete(node: Node<K, V>?, key: K): Node<K, V>? {
        //如果节点为null，直接返回null
        if (node == null) {
            return null
        }
        val cmp = key.compareTo(node.key)
        when {
            cmp < 0 -> {
                //删除左边
                node.left = delete(node.left, key)
            }
            cmp > 0 -> {
                node.right = delete(node.right, key)
            }
            else -> {
                size--
                //找到了对应点了
                //否则，先找到key对应的节点
                //否则进行删除操作

                //必须先判断右边，因为如果只有左边的话，那么把左边拿到去链接即可
                if (node.right == null) {
                    //如果右则为null，直接链接左边
                    return node.left
                }
                //如果右边不为null，左边为null,那么返回去链接上即可
                if (node.left == null) {
                    return node.right
                }
                //到这里,左右都不为null
                //1、找到目标节点的右则最小Key节点
                var miniNode = node.right
                while (miniNode?.left != null) {
                    miniNode = miniNode.left
                }
                //到这里就找到了目标节点右则节点的最小key的节点了

                //2、以目标节点右侧最小节点为接点
                //3、接点的右则为目标节点的右侧
                //4、接点的左侧为目标节点的左侧
                miniNode?.left = node.left
                miniNode?.right = node.right
                //5、接点为目标节点父节点的左侧
                //6、删除目标节点右侧最小节点
                var miniFather = node.right
                while (miniFather?.left != null) {
                    if (miniFather.left?.left == null) {
                        miniFather.left = null
                    } else {
                        miniFather = miniFather.left
                    }
                }
                return miniNode
            }
        }
        return null
    }

获取最大key的节点

最左侧的，是不是是小的呀？

    /**
     * 查找最小值key值的数据
     */
    fun miniKeyNode(): Node<K, V>? {
        //最小key值就是最左边的值
        if (root == null) {
            return null
        }
        if (root?.left == null && root?.right == null) {
            return root
        }
        var miniNode = root!!.left
        while (miniNode?.left != null) {
            miniNode = miniNode.left
        }
        return miniNode
    }

另外一种方法则是通过递归的方式查找

 /**
     * 查找最小的节点
     */
    fun miniNode(): Node<K, V>? {
        return findMiniNode(root)
    }

    /**
     * 查找当前节点以下最小key的节点
     */
    private fun findMiniNode(node: Node<K, V>?): Node<K, V>? {
        if (node == null) {
            return null
        }
        if (node.left !== null) {
            return findMiniNode(node.left)
        }
        return node
    }

查找最大key值的节点

思想跟查找最小key值节点是一样的

  /**
     * 找最大的key值
     */
    fun maxKeyNode(): Node<K, V>? {
        if (root == null) {
            return null
        }
        if (root?.left == null && root?.right == null) {
            return root
        }
        var maxKeyNode = root?.right
        while (maxKeyNode?.right != null) {
            maxKeyNode = maxKeyNode.right
        }
        return maxKeyNode
    }

递归的实现方式

    fun maxNode(): Node<K, V>? {
        return findMaxNode(root)
    }

    private fun findMaxNode(node: Node<K, V>?): Node<K, V>? {
        if (node == null) {
            return null
        }
        if (node.right != null) {
            return findMaxNode(node.right)
        }
        return node
    }

遍历

数据结构一般都提供遍历方式吧

在二叉树中，遍历方式：

• 前序遍历
• 中须遍历
• 后序遍历
• 层遍历

前序遍历

前序遍历主是先遍root，然后遍历左边，再遍历右边

代码如下：

 /**
     * 获取到Key列表:前序遍历方式，先遍历root节点，再遍历左节点，再表呢右节点
     */
    fun getPreKeyList(): List<K> {
        val keys = ArrayList<K>()
        preKeyList(root, keys)
        return keys
    }

    private fun preKeyList(node: Node<K, V>?, keys: java.util.ArrayList<K>) {
        //如果节点为null，那么就返回
        if (node == null) {
            return
        }
        //开始添加key
        keys.add(node.key)
        if (node.left != null) {
            preKeyList(node.left, keys)
        }
        //遍历右边
        if (node.right != null) {
            preKeyList(node.right, keys)
        }
    }

中序遍历

中序嘛，也就是root在中间。先遍历左边的，再到root,再到右边的。

代码如下实现：

    fun getMidKeyList(): List<K> {
        val keys = ArrayList<K>()
        midKeyList(root, keys)
        return keys
    }

    private fun midKeyList(node: Node<K, V>?, keys: java.util.ArrayList<K>) {
        if (node == null) {
            return
        }
        //先遍历左边的
        if (node.left != null) {
            midKeyList(node.left, keys)
        }
        //中间
        keys.add(node.key)
        //右边
        if (node.right != null) {
            midKeyList(node.right, keys)
        }
    }

后序遍历

会了前面两个，相信就会后序遍历了吧。

后序遍历，先遍历左边的，再到右边的，再到root

代码实现：

  fun getEndKeyList(): List<K> {
        val keys = ArrayList<K>()
        endKeyList(root, keys)
        return keys
    }

    private fun endKeyList(node: Node<K, V>?, keys: java.util.ArrayList<K>) {
        if (node == null) {
            return
        }
        if (node.left != null) {
            endKeyList(node.left, keys)
        }
        if (node.right != null) {
            endKeyList(node.right, keys)
        }
        keys.add(node.key)
    }

层遍历

层遍历的思想很简单，从第上往下，第一层开始，往下开始遍历。

先遍历当前层，然后如果当前层有左右的话，添加到一个集合/队列里，然后遍历队列里的内容，添加到集合中，再判断队列里的所有Item是否有左右，有的话继续添加到新的队列中，继续如此操作即可。

代码实现：

  fun getLayerKeyList(): List<K> {
        val keys = ArrayList<K>()
        if (root != null) {
            val layItems = ArrayList<Node<K, V>?>()
            layItems.add(root)
            layerKeyList(layItems, keys)
        }
        return keys
    }

    private fun layerKeyList(layItems: ArrayList<Node<K, V>?>, keys: java.util.ArrayList<K>) {
        val nextItems = ArrayList<Node<K, V>?>()
        layItems.forEach {
            if (it == null) {
                return
            }
            //添加到集合里
            keys.add(it.key)
            //如果有左边
            if (it.left != null) {
                nextItems.add(it.left)
            }
            if (it.right != null) {
                nextItems.add(it.right)
            }
        }
        if (nextItems.size > 0) {
            layerKeyList(nextItems, keys)
        }
        layItems.clear()
    }

获取最大深度

树结构的最大深度，指的就是层数，也就是从上往下数。

代码也不难，很简单。

    fun getDepthSize(): Int {
        return computeDepthSize(root)
    }

    private fun computeDepthSize(node: Node<K, V>?): Int {
        if (node == null) {
            return 0
        }
        var leftDepth = 0
        if (node.left != null) {
            leftDepth = computeDepthSize(node.left)
        }

        var rightDepth = 0
        if (node.right != null) {
            rightDepth = computeDepthSize(node.right)
        }

        //说明没有子节点了，算自己一层吧
        if (leftDepth == 0 && rightDepth == 0) {
            return 1
        }

        //左边大，返回左边的
        if (leftDepth > rightDepth) {
            return leftDepth + 1
        }

        //右边大返回右边的，等于随便返回一个都行的
        if (leftDepth <= rightDepth) {
            return rightDepth + 1
        }

        return 0
    }

测试

测试数据

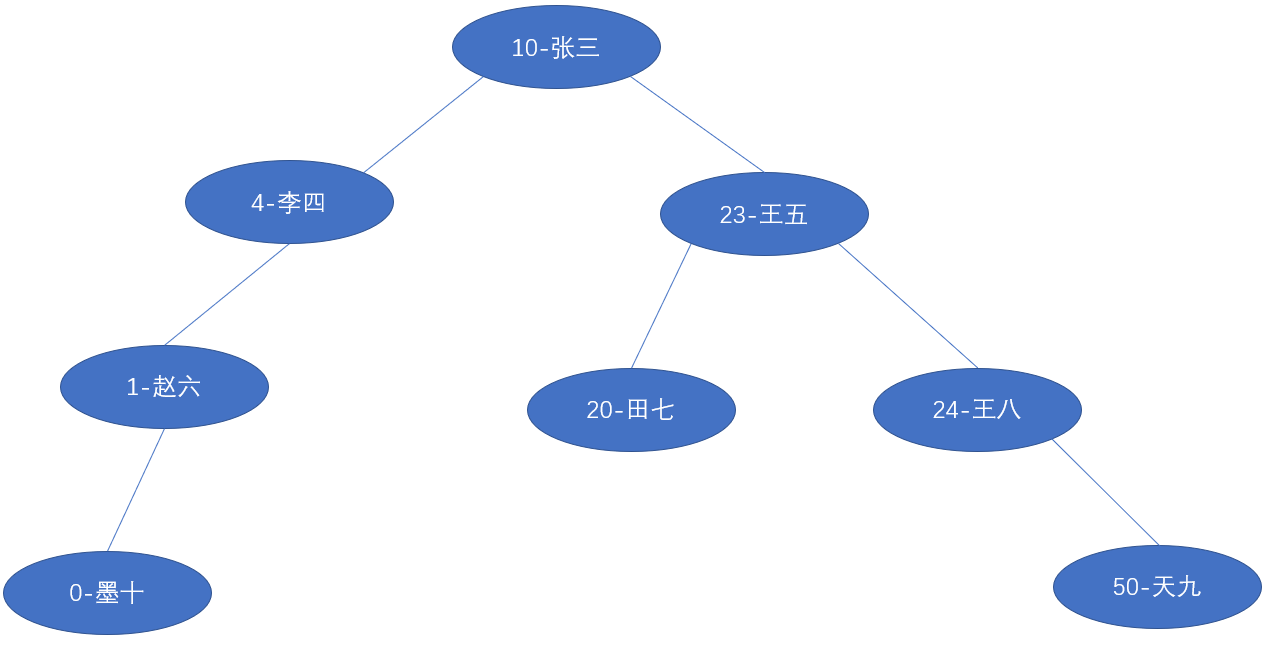
测试代码：

fun main() {
    val binaryTree = BinaryTree<Int, String>()
    binaryTree.put(10, "张三")
    binaryTree.put(4, "李四")
    binaryTree.put(23, "王五")
    binaryTree.put(24, "赵六")
    binaryTree.put(20, "田七")
    binaryTree.put(1, "王八")
    binaryTree.put(50, "天八")
    binaryTree.put(0, "墨十")
    //获取
    val result = binaryTree.get(23)
    println(result)
    //binaryTree.delete(23)
    //val deleteResult = binaryTree.get(23)
    //println(deleteResult)
    //最key值
    val maxKeyNode = binaryTree.maxKeyNode()
    val miniKeyNode = binaryTree.miniKeyNode()
    println("maxKeyNode==> $maxKeyNode")
    println("miniKeyNode==> $miniKeyNode")
    //遍历
    val preKeySet = binaryTree.getLayerKeyList()
    for (i in preKeySet) {
        println("key == > $i")
    }
    //深度
    val depthSize = binaryTree.getDepthSize()
    println("depthSize == > $depthSize")
}

输出：

key is == > 23 value is == > 王五
maxKeyNode==> key is == > 50 value is == > 天八
miniKeyNode==> key is == > 0 value is == > 墨十
key == > 10
key == > 4
key == > 23
key == > 1
key == > 20
key == > 24
key == > 0
key == > 50
depthSize == > 4

Process finished with exit code 0

以上代码实现可能与其他教程有所不同，实现方式是不唯一的。但是思想是一样的。

算法跟编程语言无关，只是思想，不同的编程语言，不同的写法也是可以实现的，效果一样即可。