全部 文章 问答 分享 共找到210个相关内容
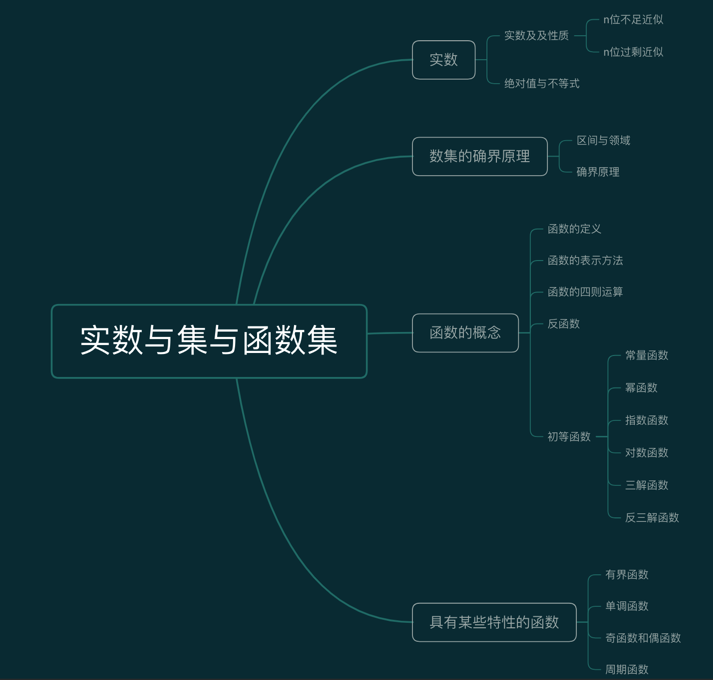
[文章] 数学分析-实数集与函数
实数集与函数实数实数由有理数和无理数两部分组成有理数:可以用分数形式p/q(p,q为整数,q!=0)来表示。也可以用有限十进制小数或者无限十进制循环小数来表示。无理数:无限十进不循环小数为无理数。有有限小数也可以表示成无限小数。比如说:2.001记为2.0009999999.....比如说:-8记为-7.9999999999.....比如说:0记为0.0000.....也就是说,任何一个实数,都可以用一个确定的无限小数来表示。n位不足近似与n位过剩近似假设X=a0·a1·a2...an为非负实数,那么我们称有理数Xn=a0·a1·a2...an为实数X的n位不足近似,而有理数Xn拔=Xn+1/10的n次方为X的n位过剩近似。什么意思呢?比如说,实数X=10.01,那么10.009999为10.01的6位不足近似。而10.01+0.02=10.02为10.01的2位过剩近似。而负实数则相反。命题:x=a0a1a2a3....an与y=a0a1a2...an为两个实数,则x>y的等价条件存在非负整数n使得xn>yn拔也就是x的n位不足近似>y的n位过剩近似。eg:设x,y为实属,x<y,证明:存在有理数r满足:x<r<y证明:由于x<y,故存在xn拔<yn,n为非负整数。令r=1/2(xn拔<+yn),由定义有理数可以表示为p/q,q不为0,q,p为整数,那么r为有理数。实数的性质实数的四则运算,加减乘除(除数不为0)是封闭的,也就是运算结果仍然是实数;实数集是有序的,也就是ab两个实九必须满足a=b,或者a>b,或者a<b;实数的大小具有传递性,也就是a>b,b>c那么a>c实数具有阿基米德性,也就是任意的实数a,b,如果b>a>0,那么存在整数n使得na>b;实数集具有稠密性,也就是说任意的两个实数间,一定存在另外一个实数,这个实数可以是有理数,也可以是无理数;实数集与数轴成映射关系,也就是所有的实数都在在数轴上找到对应的位置。阿基米德性什么是阿基米德性呢?对于任何a,b$\in$R,若b>a>0,则存在正整数n使得na>b>=(n-1)aeg:设a,b属于实数集,证明:若对任何正数ε,有a<b+ε,则a<=b这里要理解的是ε这个玩意儿,是可大可小的,所以证明时是一个好用的东西可以使用反证法来证明。若结论不成立,那么根据实数集的性质,有序性,则有a>b,令ε=a-b,则ε为正数且a=b+ε,但这与假设的a<b+ε相矛盾,所以a<=b成立。绝对值与不等式$|a|=\begin{cases}a,a>=0\-a,a<0\end{cases}$数轴上绝对值的含义数轴上绝对值的含义就是点a到原点的距离为$|a|$实数的绝对值性质$|a|$=$|-a|$>=0;当且仅当a=0时有$|a|$=0-$|a|$<=a<=$|a|$$|a|$<h$\iff$

[文章] 前端渲染文档中的数学公式
前端渲染文档中的数学公式使用mavon-editor可以很好的渲染出一篇md格式文档。但是当文档中中存在数学公式时,渲染出来的结果可能是下面这样也可能是这样然后就蒙了,这谁看得懂?

[文章] AndroidStudio构建分析
as编译代码慢不知道什么版本开始,多了一个构建分析功能。
2024-11-27 09:59
·
AndroidStudio
[问答] 无法分析主机 仓库崩了?
仓库导入依赖提示无法分析主机是仓库的问题吗我添加了阿里云的仓库代码如下://Top-levelbuildfilewhereyoucanaddconfigurationoptionscommontoallsub-projects
2020-07-06 12:30
·
领券联盟

[文章] Android 分析吃掉内存的大图片
我们可以录制某个时间段的内存记录,做分析,比如asprofiler。点击左边的录制。等待几秒后录制完成,as会自动处理结果,可以看到如下信息。
[问答] 第三方APP问题分析流程
是其他没有使用定制系统的机器所没有的,比如A机器用了定制系统,B机器没有使用定制系统,A使用微信,结果一直收不到消息,而B使用微信,是能正常收到消息的;
那我们该如何正确地分析问题呢

[文章] App内部亮度调节方案分析
分析官方提供了两种亮度调节的方式,所以有两种方案-在进退App时修改系统亮度-在当前App内反复修改当前window亮度来分析一下每一种方案的可行性在进退App时修改系统亮度这种方案的大体思路就是,先给之前的系统亮度值做记录
[分享] 带你全面分析vue-router源码(万字长文)
这篇就继续上次的话题,深入分析vue-router源码中对导航守卫、动态参数匹配、过渡效果和异步组件等的实现

[文章] 再次拜读《智慧的钥匙》
用钱老的例子来说就是算一道数学题,用经验很容易想到在问法改一改描述就能很大程度简化。用程序员的例子就是可能后端有个非常棘手的问题啊,产品经理看了一遍之后让前端改一改就好了。
2021-02-03 00:30
·
思考

[文章] 普通大三的年计划
点就是补充时间线就是如下图面就分开来说1.掌握核心知识(50%)英语,数学,数据结构/算法,编程。
2020-12-23 23:31
·
思考记录

[文章] Android xml中imageview设置src的耗时分析
总结肉眼看不出卡顿不代表卡顿,特别是tv,不像手机可以触摸如果你有台低配设备,那恭喜你,你会对卡顿更加敏感,离真相更近trace的抓取,分析
[问答] Camerax 图像分析?
如何获得camerax的视频流并进行处理
2021-09-23 16:58
·
android

[文章] Android某app环境检测分析
背景分析某银行app。
[问答] ANR问题分析
ActivityManager: Reason: Input dispatching timed out (ActivityRecord{xxx} does not have a focused window)
monkey测试测出来得ANR,有没有人知道这类ANR是什么场景发生的。

[文章] 2024.3.22FunPlus客户端开发工程师笔试记录
会有一些考数学逻辑和程序计算题,还有几道是C++的,这个确实是一点都没学过,也没办法了。不过仍然是有好几道树的问题。 填空题的话考了表达式、程序概念、程序计算、数学逻辑方面。
2024-03-25 00:50
·
笔试

[文章] 记录一次TextView超长滚动的问题
parent"app:layout_constraintTop_toTopOf="parent"/>问题原因:Marquee效果的计算逻辑与文本对齐方式的冲突,问题根源分析

[文章] 2024.3.22FunPlus客户端开发工程师笔试记录
会有一些考数学逻辑和程序计算题,还有几道是C++的,这个确实是一点都没学过,也没办法了。不过仍然是有好几道树的问题。填空题的话考了表达式、程序概念、程序计算、数学逻辑方面。
2024-03-31 00:26
·
笔试
[问答] 图凌的界面分析
老哥们图凌界面这个是什么原理,背景是我的手机桌面透明activity嘛
2020-09-20 01:00
·
android

[文章] 【完结】Android开发Jeptack系列之Navigation
Navigation与BottomNavigationView结合使用一Jetpack组件Navigation与BottomNavigationView结合使用二Jetpack组件Navigation源码分析

[文章] C语言入门(3)
大家可以在空余时间消化练习.之前的小编没排序,现在排个序:C语言入门(1)-----最简框架C语言入门(2)-----框架解析目录1.变量的命名规则2.变量的输入输出3.算术运算符4.自动类型转换与强制类型转换5.调用数学函数内容

[文章] Android 性能分析工具Simpleperf简单使用
背景Simpleperf可记录整个系统运行过程,性能损坏小,as的profiler损坏比较大。搞了一个下午一直失败,原来是app是release状态,无法抓信息。我晕。切记app必须debug状态,不要信任何博客文档说root的手机可以无视,我的就是root的,信了他们的邪!如何使用进入ndk目录例如/Users/os/Library/Android/sdk/ndk/23.1.7779620/simpleperfPython3环境进入后执行//目录/Users/os/Library/Android/sdk/ndk/23.1.7779620/simpleperfpython3app_profiler.py-pcom.hulian.newos默认10s结束,执行完成后需要拉取数据,有2种方式1,html方式查看结果//目录/Users/os/Library/Android/sdk/ndk/23.1.7779620/simpleperfpython3report_html.py完成之后在目录下有一个report.html使用浏览器打开即可。2,转换svg方式录制完成之后,执行这个命令拿到结果。//目录/Users/os/Library/Android/sdk/ndk/23.1.7779620/simpleperfpython3report_sample.py--symfsbinary_cache>out.perf下载这个工具gitclonehttps://github.com/brendangregg/FlameGraph.git把上面的out.perf文件复制到graph工具目录下,不复制也行,你知道怎么用就行。需要perl环境,mac默认有//目录FlameGraphperlstackcollapse-perf.plout.perf>out.foldedperlflamegraph.plout.folded>a.svg完成后在工具目录下会有a.svg,浏览器打开即可。

[文章] 考研与否要结合自身
考研的计算机,数学,英语与政治,我特别喜欢。我现在很多思考都类比于计算机概念。比如我觉得人就是操作系统。人的情绪要加缓存机制。人做事要加锁,做事最好是先进先出非抢占式算法。数学用于我思维与量化。
- 1
- 2
- 3
- 4
- 5
- 6
- 7